Composite transformation:
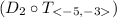
1. Translation 5 units to the left and 3 units down:
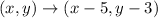
Apply the rule above to vertices of given triangle:
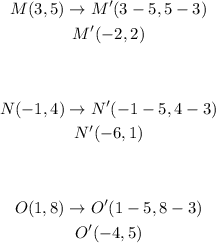
2. Dilation with factor 2:
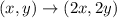
Apply the rule above to vertices M'N'O':
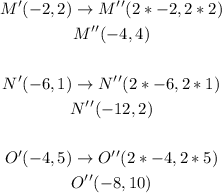
Then, the vertices of image after the composite transformation are:
M''(-4,4)
N''(-12,2)
O''(-8,10)
Graph: