Question

A community center plans to build new triangular garden outside. Triangle LNO represents the blueprint plans for the new garden. NP represents the center aisle of the garden. A) What is the length of the center aisle? Show your work.B) What is the exact length of the base of the garden? Show your work.C) What is the approximate area of the garden? Show your work. Round to the nearest hundredth square yard.

Answer 1

Answer;

A) 24 yards

B) (24 + 8√3)yards

C) 454.28 square yards

Explanations:

A) The triangle NPO is a right triangle. The length of the centre aisle NP is determined using the SOH CAH TOA identity;

`\begin{gathered} sin60=(NP)/(16√(3)) \\ (√(3))/(2)=(NP)/(16√(3)) \\ 2NP=16(3) \\ 2NP=48 \\ NP=24yds \end{gathered}`

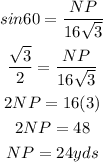
Hence the length of centre aisle is 24 yards

B) The measure of the base is LO

LO = LP + PO

Determine the length of LP and PO

`\begin{gathered} tan45=(NP)/(LP) \\ 1=(24)/(LP) \\ LP=24yds \end{gathered}`
`\begin{gathered} tan60=(NP)/(PO) \\ √(3)=(24)/(PO) \\ PO=(24)/(√(3)) \\ PO=(24√(3))/(√(3)*√(3)) \\ PO=8√(3)yds \\ \end{gathered}`
`Length\text{ of the base LO}=(24+8√(3))yds`

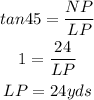
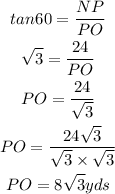
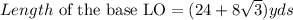
C) The area of the garden (triangle) is expressed as:

`\begin{gathered} A=(1)/(2)* base* height \\ A=(1)/(2)* LO* NP \\ A=(1)/(2)*(24+8√(3))*24 \\ A=12(24+8√(3)) \\ A=12(37.8564) \\ A\approx454.28yd^2 \end{gathered}`

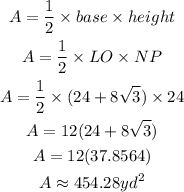
Hence the approximate area of the garden is 454.28 square yards