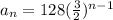Question

A geometric sequence has terms a3 = 288 and a8= 2,187. Write the explicit formula for the sequence

Answer 1

Given that,

A geometric sequence has terms a3 = 288 and a8= 2,187

we know the general term of the geometric series as,

`a_n=ar^(n-1)`

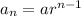
where a is the first term, r is the common ratio and n is the number of terms

we get,

`\begin{gathered} _{}a_3=ar^2 \\ 288=ar^2----(1) \end{gathered}`

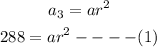
also,

`\begin{gathered} a_8=ar^7 \\ 2187=ar^7-----(2) \end{gathered}`

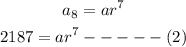
Dividing (2) by (1), we get

`(ar^7)/(ar^2)=(2187)/(288)`
`r^5=(243)/(32)`
`\begin{gathered} r^5=(3^5)/(2^5) \\ r^5=((3)/(2))^5 \end{gathered}`
`r=(3)/(2)`

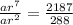
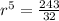
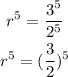
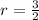
Substitute r=3/2 in equation (1) we get,

`a((3)/(2))^2=288`
`(9a)/(4)=288`
`a=(288*4)/(9)`
`a=128`

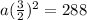
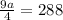
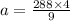
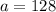
The explicit formula for the given geometric series is

`a_n=128((3)/(2))^(n-1)`

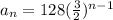
Answer is: option D:

`a_n=128((3)/(2))^(n-1)`