Question

In triangle ABC, what is the measure of b if a = 6, C = 4,

and B = 75°?

A. 5.64
B. 6.29
C. 6.78
D. 7.02

Answer 1

Given:

In triangle ABC, a = 6, c = 4, and B = 75°.

To find:

The measure of b.

Solution:

According to the Law of Cosine:

`b^2=a^2+c^2-2ac\cos B`

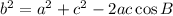
Substituting the given values in the above formula, we get

`b^2=(6)^2+(4)^2-2(6)(4)\cos (75^\circ)`

`b^2=36+16-48(0.2588)`

`b^2=52-12.4224`

`b^2=39.5776`

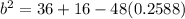
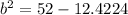
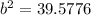
Taking square root on both sides, we get

`b=√(39.5776)`

`b=6.291073`

`b\approx 6.29`

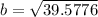
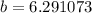
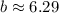
The measure of side b is 6.29 units.

Therefore, the correct option is B.