Question

Assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of O and a standard deviation of 1. Find the probability that a given score is less than -1.91

Answer 1

Given the following parameters

`\begin{gathered} \mu=0 \\ \sigma=1 \\ x=-1.91 \end{gathered}`

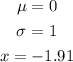
The z-score formula is given below

`z=(x-\mu)/(\sigma)`

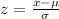
Calculate the z-score value using the above formula by substituting the parameters above

`z=(-1.91-0)/(1)=(-1.91)/(1)=-1.91`

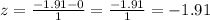
The probability that the score is less than -1.91 can be diagramatically represented as

The probability can calculated as;

[tex]\begin{gathered} Pr(z<-1.91)\Rightarrow Pr(0\le z)-Pr(0Hence, the probability that a given score is less than -1.91 is 0.0281