Question

I am stuck on 20 how do I solve for it?

Answer 1

Given the zeros of the function:

`\begin{gathered} 6 \\ 7i \\ -7i \end{gathered}`

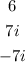
You can write the equation in Factored Form:

`f(x)=\mleft(x-6\mright)\mleft(x-7i\mright)\mleft(x+7i\mright)`

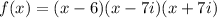
Now you need to simplify:

1. Remember this formula:

`(a+b)(a-b)=a^2-b^2`

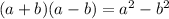
In this case:

`a=x`
`b=7i`

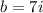
Therefore, you can rewrite the expression in this form:

`f(x)=(x-6)((x)^2-(7i)^2)`

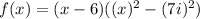
2. By definition:

`\begin{gathered} i=\sqrt[]{-1} \\ \\ i^2=-1 \end{gathered}`

Then:

`\begin{gathered} f(x)=(x-6)(x^2-49(-1)) \\ \\ f(x)=(x-6)(x^2+49) \end{gathered}`

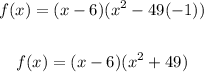
3. Now you need to use the FOIL Method in order to multiply the binomials. This states that:

`(a+b)\mleft(c+d\mright)=ac+ad+bc+bd`

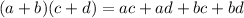
Hence:

`\begin{gathered} f(x)=(x)(x^2)+(x)(49)-(6)(x^2)-(6)(49) \\ \\ f(x)=x^3+49x-6x^2-294 \end{gathered}`

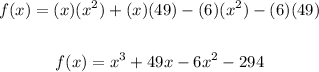
4. Ordering the polynomial from the highest power to the least power, you get:

`f(x)=x^3-6x^2+49x-294`

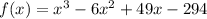
Hence, the answer is: Option d.