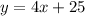Question

A phone company has a monthly data plan where a customer pays 25$ and then a certain amount of money per GB of data used on the phone. If a customer uses 3 GB, then monthly cost will be $37. If the customer uses 5 GB, then monthly cost will be $45. Find a linear equation for the monthly cost of the data plan as a function of x, the number of GB USED. C(X)=

Answer 1

Ley "x" represents the amount of extra data used in one month.

"y" represents the monthly cost.

"m" represents the slope of the linear equation, which is the cost per extra GB.

"b" represents the constant of the linear equation, in this case, the cost of the data plan.

The line can be expressed as:

`y=mx+b`

We know that the cost of the data plan is $25, this value represents the constant of the line (b)

Next, you have to determine the slope of the line.

The monthly cost after using 3GB (x) is $37 (y), this information corresponds to one ordered pair of the line (3,37)

The monthly cost after using 5GB (x) is $45 (y), this information corresponds to another ordered pair of the line (5,45)

Using both ordered pairs you can calculate the slope of the line with the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Replace the coordinates and calculate the sloe:

`\begin{gathered} m=(45-37)/(5-3) \\ m=(8)/(2) \\ m=4 \end{gathered}`

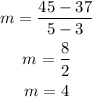
The slope of the line is m=4, this means that the monthly cost of the plan increases $4 for every extra GB used.

Now that we have calculated the slope we can determine the equation of the line:

`y=4x+25`