Question

How does a domain restriction placed on a non-invertible function affect its inverse?

Answer 1

Step-by-step explanation

The given function is a non-invertible function because it is not one-to-one. For every value of y, there are two corresponding values of x. Therefore, if we were to invert it, the result will not be a function since for each value of x there will be two values of y.

So, when the domain is restricted to [-4, ∞) then the function is invertible - note that -4 is the x-coordinate of the vertex of the parabola, so this way we will take only half of the function where it is one-to-one.

To invert it we have to solve the equation for x. First, add 1 to both sides,

`\begin{gathered} f(x)+1=(x+4)^2-1+1 \\ \\ f(x)+1=(x+4)^2 \end{gathered}`

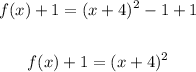
Take the square root of both sides,

`\begin{gathered} √(f(x)+1)=√((x+4)^2) \\ \\ √(f(x)+1)=x+4 \end{gathered}`

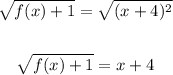
Subtract 4 from both sides,

`√(f(x)+1)-4=x`

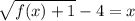
And replace x with f⁻¹(x) and f(x) with x,

`f^(-1)(x)=√(x+1)-4`

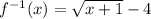
Hence, the inverse function is,

`f^(-1)(x)=√(x+1)-4`

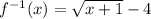
The domain of the inverse will be the range of the original function in the restricted domain. When x = -4, f(x) is -1 and as x goes to ∞, f(x) approaches ∞ as well. Hence, the domain of the inverse is [-1, ∞).