Answer:
B
Explanation:
A quadratic has a maximum value when its leading coefficient is negative, as the parabola will be curving downwards.
For A, we have the function
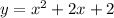
The leading coefficient here is 1, which is positive. So, A has a minimum value.
For B, we have the function
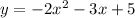
In this case, the leading coefficient is -2, which is negative. So, B is curving downwards. Therefore, it has a maximum value.
Hence, B is our correct answer.
For C and D, the leading coefficient of C is 1/2 (coefficient in front of the parentheses) and the leading coefficient of D is 1 (coefficient of the squared variable). Since both are positive, both C and D have a minimum.