Question

In a recent poll, 400 people were asked if they liked dogs, and 66% said they did. Find the margin of error of this poll, at the 90% confidence level. Give your answer to three decimals

Answer 1

Given:

sample size = 400

proportion for success p = 66% or 0.66

confidence level = 90%

Find: margin of error

Formula:

To find the margin of error of a single proportion, the formula is:

`MOE=z*\sqrt{(p(1-p))/(n)}`

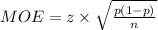
where:

z = critical value based on the given confidence level

p = proportion of success in a decimal number

n = sample size

Assuming a two-tailed test, the critical value for a 90% confidence level is 1.645. Hence, our z = 1.645.

Let's replace the variables in the formula with their corresponding numerical values based on the given information listed above.

`MOE=1.645*\sqrt{(0.66(1-0.66))/(400)}`

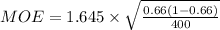
Then, solve for MOE. Here are the steps based on the formula.

1. Multiply 0.66 and the difference of 1 and 0.66.

`0.66*0.34=0.2244`

2. Divide the result by 400.

`0.2244/400=0.000561`

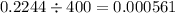
3. Get the square root of the result in step 2.

`√(0.000561)=0.023685`

4. Multiply the result in step 3 by the critical value z.

`0.023685*1.645=0.03896\approx0.039`

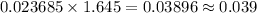
Answer:

At a 90% confidence level, the margin of error of this poll is approximately 0.039.