Question

There’s a myth that says a piece of paper cannot be folded more than seven times. In this discussion, explore this idea with your classmates.For your first post, write about your initial reaction to this idea. Address one or more of the following:Do you think this is true? Why or why not? Be specific. Have you tried folding a piece of paper more than seven times? What happened?What does paper folding have to do with exponents?

Answer 1

Step-by-step explanation

Let's assume that we want to fold a piece of paper several times. If x is the thickness of the paper then after the first fold the total thickness of the piece is doubled: 2x. If we fold it a second time now the piece is composed of four layers of paper and its thickness is 4x. After a third fold we'll have eight layers and a thickness of 8x. After a fourth fold we'll have 16 layer and a thickness of 8x. If we continue folding the piece paper we will double its thickness every time. Then we can associate the folded thickness of the piece of paper T with the original thickness x and the number of folds performed (n):

`T=2^nx`

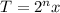
So the number of folds is the exponent of the factor 2 in the equation for the thickness of the paper. For n=7 the folded paper is 2⁷=128 times thicker than the unfolded paper so you can get an idea of why it's very difficult to fold a piece of paper more than 7 times.