Question

How do you solve this question using the beginning provided.The question is the first part of text. The second paragraph is some information on what the variable are and how their represented. The numbers at the bottom are a kind of prompt to how the answer should start.

Answer 1

According to the information given in the exercise:

- The empty tank is filled in 10 hours.

- The variable "x" represents the time (in hours) it takes pipe A to fill the tank and "y" represents the time (in hours) it takes pipe B to fill the tank.

- Pipe used A alone is used for 6 hours and then it is turned off.

- Pipe B finish filling in 18 hours (after pipe A is turned off).

By definition, these formulas can be used for Work-Rate problems:

`\begin{gathered} (t)/(t_1)+(t)/(t_2)=1 \\ \end{gathered}`
`(1)/(t_1)+(1)/(t_2)=(1)/(t)`

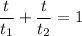
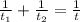
Where:

- This is the individual time for the first object:

`t_1`

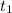
-This is the individual time for the second object:

`t_2`

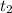
- And "t" is the time for both objects together.

In this case, having the first equation:

`(1)/(x)+(1)/(y)=(1)/(10)`

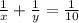
You can set up the second equation:

`(6)/(x)+(18)/(y)=1`

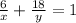
Notice that the sum of that fraction is equal to the part of the tank filled: 1 (the whole tank).

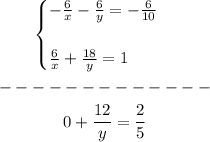
Now you can set up the System of equations:

`\begin{cases}(1)/(x)+(1)/(y)=(1)/(10) \\ \\ (6)/(x)+(18)/(y)=1\end{cases}`

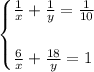
To solve it, you can apply the Elimination Method:

1. Multiply the first equation by -6.

2. Add the equations.

3. Solve for "y".

Then:

`\begin{cases}-(6)/(x)-(6)/(y)=-(6)/(10) \\ \\ (6)/(x)+(18)/(y)=1\end{cases}`
`\begin{gathered} \begin{cases}-(6)/(x)-(6)/(y)=-(6)/(10) \\ \\ (6)/(x)+(18)/(y)=1\end{cases} \\ ------------- \\ 0+(12)/(y)=(2)/(5) \end{gathered}`
`\begin{gathered} 12=(2)/(5)y \\ \\ 12\cdot5=2y \\ \\ (60)/(2)=y \\ \\ y=30 \end{gathered}`

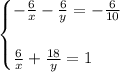
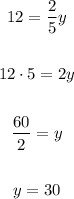
4. Substitute the value of "y" into one of the original equations.

5. Solve for "x".

Then:

`\begin{gathered} (1)/(x)+(1)/(30)=(1)/(10) \\ \\ (1)/(x)=(1)/(10)-(1)/(30) \\ \\ (1)/(x)=(1)/(15) \\ \\ (15)(1)=(1)(x) \\ x=15 \end{gathered}`

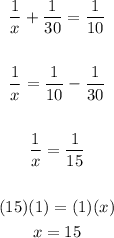
Therefore, the answer is:

- It will take pipe A 15 hours to fill the tank alone.

- It will take pipe B 30 hours to fill the tank alone.