Question

A line passes through (8,-1) and has a slope of-3/4write an equation in Ax+By=C form for this line

Answer 1

Since the given line passes through the point (8, -1) and has a slope of -3/4, then

Let us use the point-slope form of the equation

`y-y_1=m(x-x_1)`

Where:

m is the slope

(x1, y1) is a point on the line

Since m = -3/4

Since (x1, y1) = (8, -1)

Then

`\begin{gathered} y-(-1)=-(3)/(4)(x-8) \\ y+1=-(3)/(4)(x-8) \end{gathered}`

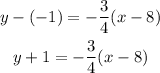
Let us simplify the right side, then put it in the form Ax + By = C

`\begin{gathered} y+1=-(3)/(4)(x)-(3)/(4)(-8)_{} \\ y+1=-(3)/(4)x+6 \end{gathered}`

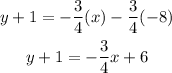
Subtract 1 from both sides

`\begin{gathered} y+1-1=-(3)/(4)x+6-1 \\ y=-(3)/(4)x+5 \end{gathered}`

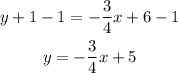
Multiply each term by 4 to cancel the denominator

`\begin{gathered} y(4)=-(3)/(4)x(4)+5(4) \\ 4y=-3x+20 \end{gathered}`

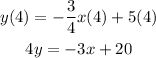
Add 3x to both sides

`\begin{gathered} 3x+4y=-3x+3x+20 \\ 3x+4y=20 \end{gathered}`

The answer is 3x + 4y = 20