Question

Consider the graph of the quadratic function y = 2x2 – 4x + 2. How many zeros does the graph have?

Answer 1

y = 2x^2 - 4x + 2

y = 2(x^2 - 2x + 1)

2(x - 1)^2 = = 0

so the graph will just touch the x axis at x = 1

So there is one zero duplicity 2.

Answer 2

The graph has:

One zero with multiplicity 2.

Explanation:

We are given a quadratic function in terms of the variable x as:

`y=2x^2-4x+2`

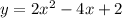
The number of zeros of this function is equal to the number of points where the graph of this quadratic function intersects the x axis and the corresponding value of x is the root of this quadratic equation.

Hence, after plotting the graph of this quadratic function we observe that the graph meets the x-axis at just one point.

Hence, the number of zeros of the graph is:

One.