Question

Graph the feasible region for the follow system of inequalities by drawing a polygon around the feasible region. Click to set the corner points.

Answer 1

First, we solve each inequality for y:

`\begin{gathered} -x+2y\ge8, \\ 2y\ge8+x, \\ y\ge(x)/(2)+4. \\ 3x+2y\le24, \\ 2y\le24-3x, \\ y\le-(3)/(2)x+12. \end{gathered}`

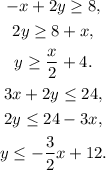
First, for -x+2y≥8 notice that all solutions (x,y) are such that y≥x/2+4, meaning that they are above the line y=x/2+4, then, the graph of the solution set of -x+2y≥8 is:

Now, for 3x+2y≤24 notice that all solutions (x,y) are such that y≤-3x/2+12, meaning that they are below the line y=-3x/2+12, then the graph of the solution set of -x+2y≥8 and 3x+2y≤24 the following intersection:

Then, we only consider the points (x,y) such that both x and y are positive numbers:

Finally, the solution set of the inequality system is:

Answer: The vertices of the solution set are (4,6), (0,12), and (0,4)