Question

Help with algebra 2 question Determine if the following sequence is arithmetic or geometric. Justify answer 27,36,48,64…Part BFind a explicit formula for the nth term of the sequence.

Answer 1

`\begin{gathered} The\text{ sequence is a geometric sequence} \\ Explicit\text{ formula = 27}*\text{ \lparen}^(4)/(3))^{n\text{ - 1}} \end{gathered}`

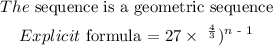
Step-by-step explanation

Given information

The given sequence is; 27, 36, 48, 64

To determine whether the given sequence is arithmetic or geometric, we will need to calculate the common difference and common ratio of the sequence.

Common difference = Next term - previous term

36 - 27 = 9

48 - 36 = 12

64 - 48 = 16

From the above calculations, you will see that the difference between the next term and the previous term is not consistent. Hence, the sequence can not be arithmetic

The next step is to determine the common ratio of the sequence

`\text{ Common ratio = }\frac{next\text{ term}}{previous\text{ term}}`
`\begin{gathered} \text{ }(36)/(27)\text{ = }(4)/(3) \\ \\ (48)/(36)\text{ = }(4)/(3) \\ \\ (64)/(48)\text{ = }(4)/(3) \end{gathered}`

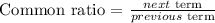
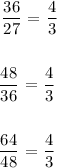
From the above calculations, you will see that the ratio of the next term to the previous term remains constant. Hence, the common ratio is 4/3. Therefore, the sequence is a geometric sequence

Part B

Find an explicit formula for the nth term of the sequence.

Since we know that the sequence is a geometric sequence, therefore, we can use the below formula to find the explicit formula

`T_n\text{ = ar}^{n\text{ - 1}}`

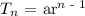
Where

a = first term of the sequence

r = common ratio of the sequence

n = number of terms

a = 27

r = 4/3

Substitute the above into the geometric sequence term

`T_n\text{ = 27}*\text{ \lparen}(4)/(3))^{n\text{ - 1}}`

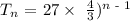
Hence, the explicit formula of the geometric sequence is

`T_n\text{ = 27 }*\text{ \lparen}(4)/(3))^{n\text{ - 1}}`