Question

The Nut Shack sells hazelnuts for $6.50 per pound and peanuts nuts for $4.70 per pound. How much of each type should be used to make a 36 pound mixture that sells for $5.40 per pound?Round answers to the nearest pound.

Answer 1

Given:

Hazelnuts sells for $6.50/pound and peanuts nuts sells for $4.70/pound

Let the number of pounds of Hazelnuts be x and the number of pounds of peanut nuts be y

The company wants a 36 pound mixture. We can write this mathematically as:

`x\text{ + y = 36}`

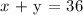
The mixture sells for $5.40 per pound. We can write this mathematically as:

`\begin{gathered} 6.50x\text{ + 4.70y = 5.40}*\text{ 36} \\ 6.50x\text{ + 4.70y = }194.4 \end{gathered}`

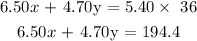
Solving the equations simultaneously using a graphical approach.

Using a graphing tool, the graph of the equations is shown below:

The point of intersection of the lines is (14, 22)

We can conclude that the company would need 14 pounds of