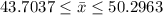Question

If n=21, ¯x (x-bar)=47, and s=6, find the margin of error at a 98% confidence level

Answer 1

The margin of error formula is given by

`T_c*\frac{s}{\sqrt[]{n}}`

where T_c is the critical T-value for n=21 degrees of freedom and s is the standard deviation. Then, for n=21 and 98% confidence level, we have that

`T_c=2.5176`

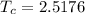
Therefore, by substituting these values into the margin of error formula, we have

`T_c*\frac{s}{\sqrt[]{n}}=2.5176*\frac{6}{\sqrt[]{21}}`

which gives

`T_c*\frac{s}{\sqrt[]{n}}=3.2963`

Then, the margin of error is 3.2963 and the confidence interval for the given mean is:

`43.7037\le\bar{x}\le50.2963`