Question

HELP ASAP PLEASEEEE..OSHA safety regulations require that the base of a ladder be placed 1 ft from the wall for every 3 ft of ladder length. To the nearest tenth of a degree, find the angle that the ladder forms with the ground and the angle that it forms with the wall.What angle does the ladder form with the ground ?? What angle does it form with the wall??

Answer 1

Rough diagram:

Given ladder is 1 feet from wall FOR EVERY 3 feet length of ladder. No matter what the length of ladder is, it needs to keep this ratio. So, we drew a triangle to find the angles. No matter what is the length of ladder [keeping ratio of distance from wall] , we will get the same angle.

We need to use trigonometry to solve the rest of the question.

First,

What angle does the ladder form with the ground ??

This is labeled as "x". The adjacent side and hypotenuse to x are known, so we have to use cosine to solve for x. Shown below:

`\begin{gathered} \cos (x)=(1)/(3) \\ x=\cos ^(-1)((1)/(3)) \\ x=70.53 \end{gathered}`

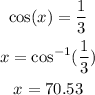
The angle, x, is 70.53 degrees.

What angle does it form with the wall??

This is labeled as "y". The opposite and hypotenuse to y are known, so we have to use sine to solve for y. Shown below:

`\begin{gathered} \sin (y)=(1)/(3) \\ y=\sin ^(-1)((1)/(3)) \\ y=19.47 \end{gathered}`

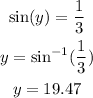
The angle, y, is 19.47 degrees.