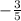Question

The equation of line m is 5x−3y=2. What is the slope of a line that is perpendicular to line m? Enter your answer in the box.

Answer 1

-3y=-5x+2
y=-5/-3x+2/-3
y=5/3x-2/3
compare y=mx+c || m =5/3
for perpendicularity
m=-1/M
m=-1/5/3
m= -3/5

Answer 2

Step 1

Find the slope of the line M

we have

`5x-3y=2`

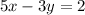
isolate the variable y

`3y=5x-2 \\ \\y=(5)/(3)x-(2)/(3)`

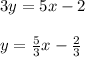
the slope of the line is
`(5)/(3)`

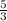
Step 2

Find the slope of the line perpendicular to line M

we know that

if two lines are perpendicular , then the product of their slopes are equal to minus one

so

`m1*m2=-1`

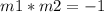
we have

`m1=(5)/(3)`

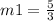
Find m2

`m2=-1/m1`

`m2=-1/(5/3)`

`m2=-(3)/(5)`

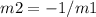
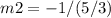
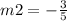
therefore

the answer is

`-(3)/(5)`