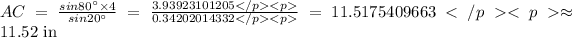Question

In ΔABC, BC = 4 centimeters, m∠B = m∠C, and m∠A = 20°. What is AC to two decimal places?

A.9.32 centimeters

B.10.01 centimeters

C.11.52 centimeters

D.12.09 centimeters

Answer 1

m<A = 20°
m<B = m<C = 80°

Law of Sines , in any triangle we have
a/sin A = b/sin B = c/sin c

4/sin20 = AC/sin80 = AB/sin80

now we can solve AC

4/sin20 = AC/sin80
AC = 4 (sin80)/ sin20
AC = 4(0.98) / (0.34)
AC = 3.92 / 0.34
AC = 11.52

answer

C.11.52 centimeters

Answer 2

C.11.52 centimeters

Explanation:

Given,

In triangle ABC,

BC = 4 centimeters, m∠B = m∠C, and m∠A = 20°.

Since, the sum of all interior angles of a triangle is supplementary,

⇒ m∠A + m∠B + m∠C = 180°

⇒ 20° + m∠B + m∠B= 180°

⇒ 2 m∠B = 160°

⇒ m∠B = 80°,

Now, By the law of sines,

`(sin A)/(BC)=(sin B)/(AC)`

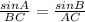
By cross multiplication,

`sin A* AC = sin B* BC`

`\implies AC = (sin B* BC)/(sin A)`

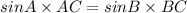
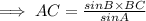
By substituting values,

`AC=(sin 80^(\circ)* 4)/(sin 20^(\circ))=(3.93923101205</p><p>)/(0.34202014332</p><p>)=11.5175409663</p><p>\approx 11.52\text{ in}`