Question

two cyclists start at the same point and travel in opposite. directions. one cyclist travels 5 mi/h slower than the other. two cyclists are 185 miles apart after 5 hours, what is the rate of each cyclist?

Answer 1

• The rate of the first cyclist is 21 mi/h

,

• The rate of the second cyclist is 16 mi/h.

Explanation:

• Let the rate of the first cyclist = x mi/h.

One cyclist travels 5 mi/h slower than the other, therefore:

• The rate of the second cyclist = (x-5) mi/h.

`\begin{gathered} \text{Distance}=\text{Rate}* Time \\ \text{The distance covered by the first cyclist: }d_1=5x \\ \text{The distance covered by the }\sec ond\text{ cyclist: }d_2=5(x-5) \end{gathered}`

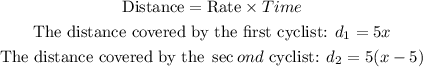
The distance between the two cyclists = 185 miles.

Since they move in opposite directions, we add the distances.

`\begin{gathered} 5x+5(x-5)=185 \\ 5x+5x-25=185 \\ 10x=185+25 \\ 10x=210 \\ x=210/10 \\ x=21\text{ mi/h} \end{gathered}`

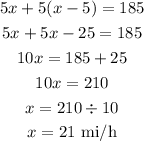
Therefore, the rate of the first cyclist is 21 mi/h and the rate of the second cyclist is 16 mi/h.