Question

Identify the vertical asymptotes, horizontal asymtope, domain, range. Then Sketch the grapgh.

Answer 1

Since the denominator cannot be 0, the domain of the graph is the set of real numbers except for -1.

`D\colon\mleft\lbrace x|x\in\R\text{ except -1}\mright\rbrace`

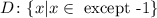
This means the vertical asymptote is

`x=-1`

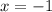
Since the value of f(x) is 3 over any non-zero number, the range of the function is the set of real numbers except for 0.

`R\colon\mleft\lbrace y\mright|y\in\R\text{ except 0}\}`

This means the horizontal asymptote of the graph is

`y=0`

To sketch the graph, substitute the different values of x into the equation and then solve for f(x)=y. Create a table of values and then plot the points on the Cartesian coordinate system.

Here are the points on the left part of the graph.

`(-10,(1)/(3)),(-3,1.5)\text{, }\cdot(-1.3,10)`

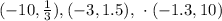
Here are the points on the right part of the graph.

`(-0.7,-10),(0,-3),(10,-0.273)`

Draw a curve passing through the points for the left part of the graph. Draw a curve passing through the points for the right part of the graph. Thus, the graph is as follows.

Make sure that the graph does not intersect the obtained asymptotes.