Question

Keith's florists has 15 delivery trucks, used mainly to deliver flowers and flower arrangements in the greenville, south carolina, area. of these 15 trucks, 5 have brake problems. a sample of 4 trucks is randomly selected. what is the probability that 2 of those tested have defective brakes?

Answer 1

Hence, the probability is:

0.296

Explanation:

This can be solved with the help of the binomial probability as:

`P(x=r)=n_C_rp^r(1-p)^(n-r)`

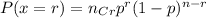
where n denote the quantity which are chosen.

r denote the quantity whose probability is to be determined or success.

and p denote the probability of success.

with n=4 since 4 trucks are randomly selected.

p=5/15=1/3 ( As 5 have brake problems out of total 15 trucks)

1-p=10/15=2/3

r=2 ( since we are asked to find the probability that 2 of those tested have defective brakes)

Hence, the probability is:

`P(x=2)=4_C_2((1)/(3))^2((2)/(3))^2\\\\\\P(x=2)=(4!)/(2!* (4-2)!)* (1)/(9)* (4)/(9)\\\\\\P(x=2)=0.296`

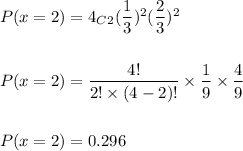
Hence, the probability is:

0.296

Answer 2

Given the fact that 5 out of the 15 trucks have brake problems, we can find the probability that a delivery truck has brake problems as 5/15 = 0.3333. In the sample of 4 trucks, the number of trucks that have defective brackets is a binomially distributed random variable with n = 4 and p = 0.3333. Using the formula for binomial distribution, we get P(X = 2) = 4C2 * 0.3333² * (1–0.3333)² = 0.2963.
The answer is 0.2963.