Answer:
f(x), h(x) and k(x) can not be an exponential function.
Step-by-step explanation:
A exponential function can be represented by:
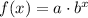
Let's evaluate each function and see which of the functions fit the expression above.
First, let's evaluate x = 0
For x = 0
f(x) = 3
g(x) = 1
h(x) = 1
k(x) = 0
If we substitute x=0 in the expression above, we will find that:
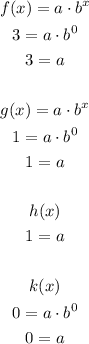
To be consider a exponential function, a can not be zero. Thus, k(x) can not be an exponential function
Now, we already now the value for "a". The next step is to find the value for b:
Let's evaluate x = 1
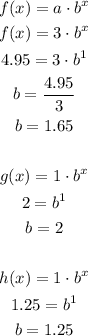
Now, we can write all the posible exponential functions. Then, we can test the other given points:
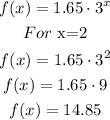
As we can see, f(x) in not an exponential function.
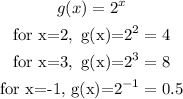
All the points are the same as the presented in the table.
As we can see, g(x) can be an exponential function.
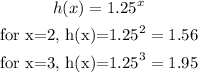
As we can see, g(x) can not be an exponential function.