Question

I need help solving this practice I’m having trouble with it

Answer 1

From the problem, we have :

`2\sin ^2x+5\sin x-3=0`

Let m = sin x

`2m^2+5m-3=0`

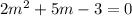
Factor completely :

`\begin{gathered} 2m^2+5m-3=0 \\ (2m-1)(m+3)=0 \end{gathered}`

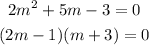
Equate factors to 0 then solve for m :

`\begin{gathered} 2m-1=0 \\ 2m=1 \\ m=(1)/(2) \\ \\ m+3=0 \\ m=-3 \end{gathered}`

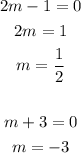
Bring back m = sin x :

`\begin{gathered} m=(1)/(2)\Rightarrow\sin x=(1)/(2) \\ m=-3\Rightarrow\sin x=-3 \end{gathered}`

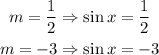
Note that the sin of an angle is ranging from -1 to 1, so sin x = -3 is invalid. Therefore, neglect sin x = -3 and use sin x = 1/2 only.

`\begin{gathered} \sin x=(1)/(2) \\ \text{take arcsin :} \\ \arcsin (\sin x)=(1)/(2) \\ x=30\quad \text{and}\quad 150 \end{gathered}`

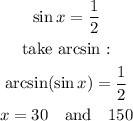
Convert 30 and 150 degrees to radians :

`\begin{gathered} 30*(\pi)/(180)=(\pi)/(6) \\ 150*(\pi)/(180)=(5\pi)/(6) \end{gathered}`

Note that 2π is one full circle.

So we can add it to the solution.

That will be :

`\begin{gathered} (\pi)/(6)+2\pi n \\ \text{and} \\ (5\pi)/(6)+2\pi n \end{gathered}`

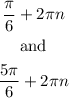
ANSWERS :

`\begin{gathered} (\pi)/(6)+2\pi n,\quad \text{ where n is an integer} \\ \text{and} \\ (5\pi)/(6)+2\pi n,\quad \text{ where n is an integer} \end{gathered}`