Question

14. A volleyball is hit upward by a player in a game. The height h (in feet) of the volleyball after t (seconds) is given by h (t) = -5ť^2 + 30t + 6.

Answer 1

We have that the function that represents this situation is:

`h(t)=-5t^2+30t+6`

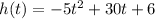
notice that we have a quadratic function, then, we can find the maximum height by finding the vertex of the parabolla. To find the vertex, we can use the following general rule:

`\begin{gathered} f(x)=ax^2+bx+c \\ vertex\colon(-(b)/(2a),f(-(b)/(2a))) \end{gathered}`

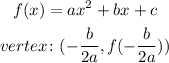
in this case, we have the following coefficients:

`a=-5,b=30,c=6`

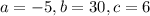
then, the x coordinate of the vertex is:

`-(b)/(2a)=-(30)/(2(-5))=-(30)/(-10)=3`

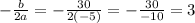
finally, we can evaluate f(3) to find the y-coordinate:

`\begin{gathered} f(-(b)/(2a))=f(3)=-5(3)^2+30(3)+6=-5(9)+90+6 \\ =-45+96=51 \end{gathered}`

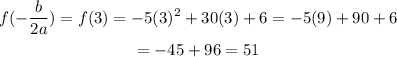
we have that f(3) = 51. This means that at time t = 3 seconds, the volleyball reaches its maximum height of 51ft