Question

Determine the zeros of the given polynomial function and the multiplicity of each zero. List the zeros from smallest to largest. If the zero is not an integer then use a fraction (not a decimal).G(x)=3x^4+6x^3+3x^21st zero = Answer for part 1 with a multiplicity of Answer for part 22nd zero = Answer for part 3with a multiplicity of Answer for part 4

Answer 1

If a polynomial can be factored as the product of k linear factors with exponents n₁, n₂, ..., n_k, as follows:

`P(x)=C\cdot(x-a_1)^(n_1)*(x-a_2)^(n_2)*\ldots*(x-a_k)^(n_k)`

Then, the zeros of P(x) are a₁, a₂, ...,a_k and their respective multiplicities are n₁, n₂, ..., n_k.

For the given polynomial, notice that 3x^2 is a common factor for all three terms. Then, factor it out:

`\begin{gathered} G(x)=3x^4+6x^3+3x^2 \\ \Rightarrow G(x)=3x^2(x^2+2x+1) \end{gathered}`

The factor (x^2+2x+1) is a perfect square binomial that can be expressed as a binomial squared:

`x^2+2x+1=(x+1)^2`

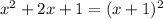
Then, G(x) can be written as:

`\begin{gathered} G(x)=3x^2(x+1)^2 \\ \Rightarrow G(x)=3(x-0)^2(x-\lbrack-1\rbrack)^2 \end{gathered}`

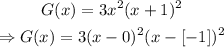
As we can see from the expression, the roots of G(x) from the smallest to largest are -1 and 0, and the multiplicities are 2 in both cases.

Therefore, the first zero is -1 with a multiplicity of 2, and the second zero is 0 with a multiplicity of 2.