To factor the expression ax² + bx + c, we can use the quadratic formula:
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zndalnwykxb6ptn1p38z.png)
where x1, and x2 are the zeros, or roots, of the polynomial. And the factored expression will be:
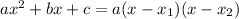
For example, if the expression is 5x² -35x + 60, then a = 5, b = -35 and c = 60. Substituting into the formula we get:
![\begin{gathered} x_(1,2)=\frac{-(-35)\pm\sqrt[]{(-35)^2-4\cdot5\cdot60}}{2\cdot5} \\ x_(1,2)=\frac{35\pm\sqrt[]{25}}{10} \\ x_1=(35+5)/(10)=4 \\ x_2=(35-5)/(10)=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ixf0n9wgr14r37ojabel.png)
Then, the factored expression is:
5x² -35x + 60 = 5(x - 4)(x - 3)