Question

A school is installing a flagpole in the central plaza. The plaza is a square with side length 100 yards asshown in the figure below. The flagpole will take up a square plot in the middle of the plaza and its bastwill have an area of x^2-8x+ 16yd^2Area of the flagpole plot: x^2-8x+16Find the length of the base of the flagpole by factoring. (Hint: Because the area of the flagpole isexpression that involves the variable 2, the length of the base will also involve the variable 2.)

Answer 1

The length base of the flag pole is (x - 4)

Explanation:

From the question provided, you can see that the central plaza is a square and a flag pole will take up a square plot in the middle of the plaza.

The area of the flag pole is given below as

`\text{Area o flagpole = x}^2-8x+16\text{ square yds}`

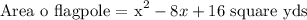
The length of the plaza is 100 yds has given from the question provided

The next thing is to factorize the above quadratic function

`\begin{gathered} \text{Area = x}^2\text{ - 8x + 16} \\ \text{Area = x}^2\text{ - 4x - 4x + 16} \\ \text{Area = x(x - 4) - 4(x - 4)} \\ \text{Area = (x - 4)(x - 4)} \\ \text{Area = (x - 4)}^2 \end{gathered}`

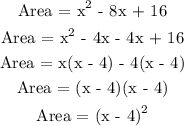
Recall that, Area of a square is equivalent to the square of its given length

Hence,

`\begin{gathered} \text{Area = length }\cdot\text{ length} \\ \text{Area = length}^2 \\ \text{ Recall that, area = (x - 4)}^2 \\ (x-4)^2=length^2 \\ \text{Take the square roots of both sides} \\ \sqrt[]{(x-4)^2}\text{ = }\sqrt[]{(length)^2} \\ \text{Length = x- 4} \end{gathered}`

Hence, the length base of the flag pole is (x - 4)