Given that the first term of a GP is -20 and the 10th term is 10240.
We need to find S11 of this GP.
The first term is a = -20 and the tenth term is ar^9 = 10240. So,
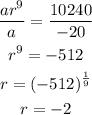
We know that the sum of n terms of gp is given by:
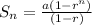
The sum of 11 terms of the gp is:
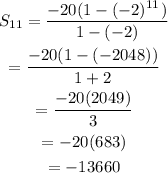
Thus, the value of S11 is -13660.