It + 3I is called absolut value which means the value of t + 3 is always positive
So we will solve two inequalities
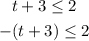
Let us solve the first one
Subtract from both sides 3
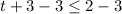

Now we will solve the second one
We multiply the bracket by (-)
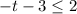
Add 3 to both sides

We will divide both sides by -1 the coefficient of t, but we must reverse the sign of the inequality because 2 < 3 if we divide both sides by -1 it will be -2 < -3 which is wrong -2 > -3, so
When you multiply or divide an inequality by negative number you must reverse the sign of the inequality
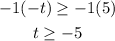
Now we will write the both inequalities togather
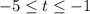
The minimum value is -5
The maximum value is -1