We have a series: 2 1/2, 3 3/4, ...
We can consider this is a arithmetic series, so it has a common difference. This difference can be calculated as:
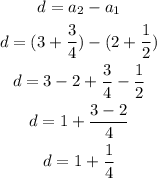
We then can consider that each term adds 1 1/4 to the previous term.
We can calculate the third and fourth term of the series as:
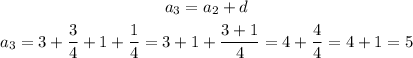
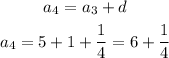
Answer: the third term is 5 and the fourth term is 6 1/4.