Question

Two health clubs offer different pricing plans for their members. Both health clubs charge a one-time sign-up fee and a monthly membership fee. The equation y=33x+45y=33x+45 represents what Health Club B charges. The table below represents what Health Club A charges.

Health Club A
Months (x) Total Cost (y)
66 225
11 400
16 575
21 750
Use the dropdown menu and answer-blank below to form a true statement.

Health Club A costs $ in monthly membership fees than Health Club B.
PLEASE ANSWER IM BEGGING YOU :(

Answer 1

I think that is is number 3

Answer 2

"Health Club A costs $2 more in monthly membership fees than Health Club B."

Let's compare the monthly membership fees of Health Club A and Health Club B based on the provided information.

For Health Club A, the equation seems to be linear. We can find the slope (m) and y-intercept (b) using the given points (x, y) from the table.

Let's use the points (11, 400) and (16, 575) to find the slope (m):

`m= (y_2 -y_1)/(x_2 -x_1)`

`m = (575 -400)/(16-11) = (175)/(5) = 35`

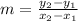
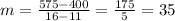
Now, we can use the slope and one point (let's use the point (11, 400)) to find the y-intercept (b) using the equation

y=mx+b:

400=35(11)+b

Solving for b:

b=400−35(11)=400−385=15

So, the equation for Health Club A is y=35x+15.

Now, let's compare the monthly membership fees of Health Club A and Health Club B:

Health Club A:

y=35x+15

Health Club B:

y=33x+45

Now, complete the sentence:

"Health Club A costs $ \underline{\hspace{2cm}} in monthly membership fees than Health Club B."

To fill in the blank, we need to subtract the corresponding coefficients of x in the two equations. In this case, it's 35−33, which equals 2. Therefore, the completed sentence is:

"Health Club A costs $2 more in monthly membership fees than Health Club B."