Question

Solve each equation some solutions will be expressed using log notation question 6 7 and 8

Answer 1

`\begin{gathered} 5)2.498 \\ 6)2.6 \\ 7)3 \\ 8)2 \end{gathered}`

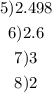
5) In this one, let's take the logarithm on both sides:

`\begin{gathered} 10^x=315 \\ \log_(10)10^x=\log_(10)315 \\ x=2.498 \end{gathered}`

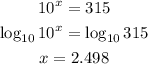
6) Let's begin this exponential equation by simplifying it whenever possible:

`\begin{gathered} 2*10^x=800 \\ (2*10^x)/(2)=(800)/(2) \\ 10^x=400 \end{gathered}`

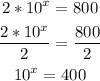
Note that we cannot rewrite 400 as a power of base 10, so let's resort to the logarithm:

`\begin{gathered} \log_(10)10^x=\log_(10)400 \\ x=2.60 \end{gathered}`

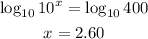
Note that according to the property of the logarithm, we can tell that log_10(10)^x is equal to x

7)

`\begin{gathered} 10^(\left(1.2x\right))=4000 \\ \log_(10)10^(1.2x)=\log_(10)4000 \\ 1.2x=3.60 \\ (1.2x)/(1.2)=(3.6)/(1.2) \\ x=3.00 \end{gathered}`

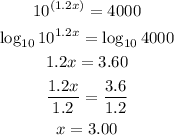
Note that in this case, we had to take the logarithms on both sides right away.

8)

`\begin{gathered} 7*10^(0.5x)=70 \\ (7*10^(0.5x))/(7)=(70)/(7) \\ 10^(0.5x)=10 \\ 0.5x=1 \\ (0.5x)/(0.5)=(1)/(0.5) \\ x=2 \end{gathered}`

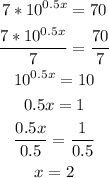
Note that in this case, after dividing both sides by 7 we ended up with two powers of base 10.