Hello there. To solve this question, we have to remember some properties about logarithms.
Given the expression:

We want to rewrite it as a single logarithm.
For this, remember the following rules:
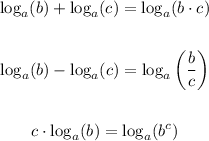
In this case we apply the third rule to the middle logarithm in order to get:
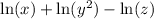
Apply the first and second rules

This is the answer to this question and it is contained in the first option.