Question

See figure below. Round answer to the nearest tenth of a degree

Answer 1

`\begin{equation*} 109.2\degree \end{equation*}`

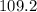
Step-by-step explanation

We want to find the measure of angle B.

To do this, we first have to find the measure of angle C using the sine rule:

`(\sin C)/(AB)=(\sin A)/(BC)`

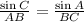
Substitute the given values into the equation and solve for C:

`\begin{gathered} \sin C=(AB*\sin A)/(BC) \\ \\ \sin C=(180*\sin42)/(250) \\ \\ \sin C=(120.4435)/(250)=0.4818 \\ \\ C=\sin^(-1)(0.4818) \\ \\ C=28.8\degree \end{gathered}`

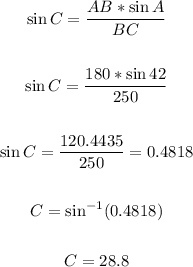
Now, we can find the measure of angle B using the sum of angles in a triangle. The sim of angles in a triangle is 180 degrees. This implies that:

[tex]\begin{gathered} That is the measure of angle B.