Question

Yvonne has started a business out of her home, where she sells hand-crafted lamp shades. Her weekly income can be modeled by the function p(x) = -2x2 + 75x, where x is the number of lamp shades produced in a week. What is the maximum revenue she earns in a week?

Answer 1

Yvonne has started a business out of her home, where she sells hand-crafted lamp shades. Her weekly income can be modeled by the function p(x) = -2x2 + 75x, where x is the number of lamp shades produced in a week. What is the maximum revenue she earns in a week?​

we have that

p(x)=-2x^2+75x -----> is a vertical parabola, open downward

the vertex is a maximum

so

Convert the quadratic equation into vertex form

y=a(x-h)^2+k

where

(h,k) is the vertex

Complete the squares

so

`\begin{gathered} p(x)=-2x^2+75 \\ p(x)=-2(x^2-37.5) \\ p(x)=-2(x^2-18.75+351.5625-351.5625) \\ p(x)=-2(x^2-18.75+351.5625)+703.125 \\ p(x)=-2(x-18.75)^2+703.125 \end{gathered}`

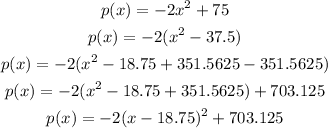
the vertex is the point (18.75,703,125)

therefore

the maximum revenue she earns in a week is $703.13