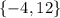Question

Find all the values of x satisfying the given conditions y = |8 - 2x| and y = 16

Answer 1

We are given the following function:

`y=\lvert{8-2x}\rvert`

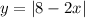
We are asked to determine the values of "x" for which "y = 16". To do that we will set the function equal to 16:

`\lvert{8-2x}\rvert=16`

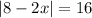
Now, to solve the equation we will use the fact that the absolute value has two possible values, a positive and a negative value. For the positive value we have:

`8-2x=16`

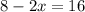
Now, we solve for "x". First, we subtract 8 from both sides:

`\begin{gathered} -2x=16-8 \\ -2x=8 \end{gathered}`

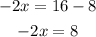
Now, we divide both sides by -2:

`x=(8)/(-2)=-4`

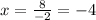
Therefore, the first possible solution is "x = -4".

For the negative form of the function we have:

`-(8-2x)=16`

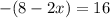
Now, we multiply both sides by -1:

`8-2x=-16`

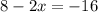
Now, we subtract 8 from both sides:

`\begin{gathered} -2x=-16-8 \\ -2x=-24 \end{gathered}`

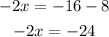
Now, we divide both sides by -2:

`x=-(24)/(-2)=12`

The second value is 12. Therefore, the solution set is:

`{}{}\lbrace-4,12\rbrace`