Question

Determine if the following equation is linear. If the equation is linear, convert i to standard form: ax+by=c

Answer 1

The standard form of the linear equation is:

`\[ 3x + 20y + 89 = 0 \]`

Therefore, option A is correct

The image shows an equation:

`\[(10 + y)^2 - y^2 = -3x + 11\]`

We need to determine whether this equation is linear or not. An equation is linear if it can be written in the form
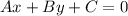`\( Ax + By + C = 0 \)`, where
`\( A \)`,
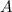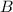`\( B \)`, and
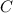`\( C \)` are constants, and there are no products or powers of the variables.

To analyze this, we'll simplify the given equation by expanding the squared term, combining like terms, and then seeing if it can be written in a linear form.

Let's start by expanding and simplifying the equation.

After expanding and simplifying the left side of the equation, we get:

`\[(10 + y)^2 - y^2 = 20y + 100\]`

So the original equation becomes:

`\[20y + 100 = -3x + 11\]`

To determine if this equation is linear, let's rearrange it into the standard form
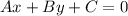`\( Ax + By + C = 0 \)` by moving all terms to one side of the equation.

The equation rearranged into the standard form is:

`\[ 3x + 20y + 89 = 0 \]`

This is indeed a linear equation because it is in the form
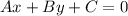`\( Ax + By + C = 0 \)` and does not contain any products or powers of
`\( x \)` or
`\( y \)`.

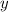The standard form of the linear equation is:

`\[ 3x + 20y + 89 = 0 \]`

Hence, the given equation is linear.

Answer 2

Given the equation:

`(10+y)^2-y^2=-3x+11`

Then, expanding and operating this equation leads to:

`\begin{gathered} 10^2+2\cdot10\cdot y+y^2-y^2=-3x+11 \\ 100+20y=-3x+11 \end{gathered}`

There are no quadratic terms, so the equation is linear. Now, converting it to standard form:

`20y+3x=-89`