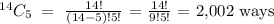Question

Suppose we have 5 colors, without replacement, from 14 distinct colors.1. If the order is not taken into consideration how many ways can this be done?2. If the order is taken into consideration how many ways?

Answer 1

1) 240,240 ways

2) 2,002 ways

Step-by-step explanation:

Here, we want to calculate the number of ways we can make a selection:

1. With the order not taken into consideration, we use the permutation formula as follows:

`^nP_r=(n!)/((n-r)!)_{}`

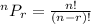
With respect to the given question, n is 14 and 5 is r

Thus, we have it as:

`^(14)P_5\text{ = }(14!)/((14-5)!)\text{ = }(14!)/(9!)\text{ = 240,240 ways}`

2. With the order taken into consideration, we use the combination formula as follows:

`^nC_r\text{ = }(n!)/((n-r)!r!)`

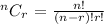
Thus, we have it as:

`^(14)C_{5\text{ }}=\text{ }(14!)/((14-5)!5!)\text{ = }(14!)/(9!5!)\text{ = 2,002 ways}`