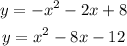
start by making both expressions equal
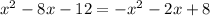
bring all to one side
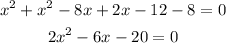
use the quadratic formula to solve the quadratic equation using a as 2, b as -6, and c as -20.
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
then,
![\begin{gathered} x=\frac{-(-6)\pm\sqrt[]{(-6)^2-4\cdot(2)(-20)}}{2\cdot2} \\ x=\frac{6\pm\sqrt[]{36+160}}{4} \\ x=\frac{6\pm\sqrt[]{196}}{4} \\ x=(6\pm14)/(4) \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zj7vgrl2pkpvms9euvqo.png)
since the expression is a quadratic equation there are going to be two possible solutions
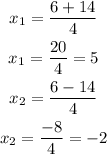
then, replace both -2 and 5 into one of the equations
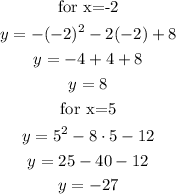
the solutions to the system are (-2,8) and (5,-27)