Let's define the following variables:
x = number of adult tickets sold
$3 = price per adult ticket
y = number of student tickets sold
$2 = price per student ticket
If a total of 200 tickets were sold, then we can say that x + y = 200. This will be our equation 1.
If the total income is $475, then 3x + 2y = 475. This will be our equation 2.
So, we have a system of equations here.
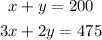
Let's solve for the value of x using the substitution method.
1. Let's rewrite equation 1 into y = 200 - x.
2. Let's replace the "y" variable in equation 2 with "200 - x".
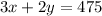
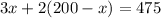
3. Let's solve for x.
Multiply 2 by the terms inside the parenthesis.
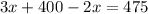
Combine similar terms like 3x and -2x.
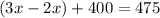
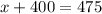
Subtract 400 on both sides of the equation.
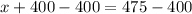
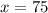
The value of x is 75.
Since x is the number of adult tickets sold, then there were 75 adult tickets sold for the high school concert.