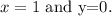Question

Solve this system using any method15y-3=-3x6x-2y=6

Answer 1

Dividing the first equation by -3 we get:

`\begin{gathered} (15y-3)/(-3)=(-3x)/(-3), \\ (15y)/(-3)-(3)/(-3)=(-3x)/(-3), \\ -5y+1=x\text{.} \end{gathered}`

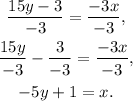
Substituting x=-5y+1 in the second equation we get:

`6(-5y+1)-2y=6.`

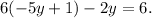
Applying the distributive property we get:

`\begin{gathered} 6*(-5y)+6*1-2y=6, \\ -30y+6-2y=6. \end{gathered}`

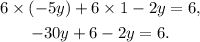
Adding like terms we get:

`-32y+6=6.`

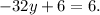
Subtracting 6 from the above equation we get:

`\begin{gathered} -32y+6-6=6-6, \\ -32y=0. \end{gathered}`

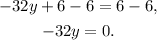
Dividing the above equation by -32 we get:

`\begin{gathered} (-32y)/(-32)=(0)/(-32), \\ y=0. \end{gathered}`

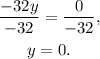
Finally, substituting y=0 in x=-5y+1 we get:

`\begin{gathered} x=-5\cdot0+1 \\ =0+1=1. \end{gathered}`

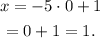
Answer: The solution to the given system of equations is:

`x=1\text{ and y=0.}`