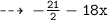Answer:
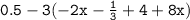
» First solve the bracket by simplification rule. Arrange x terms together and constants together.
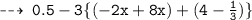
» Then solve the sub brackets in the parent bracket:
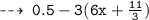
» Open the bracket following distributive property [ Multiply -3 to each constant in the bracket ]

» Then simplify: