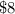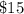Question

The inequality x < 9 or x ≥ 14 can be used to represent the hourly wage, x, of each employee at a store. Which are possible values for x? Check all that apply. $8 $9 $11 $13 $14 $15

Answer 1

x < 9...this is saying the hourly wage is less then 9 (not including 9)
x > = 14...this is saying the hourly wage is 14 and above

so possible values are : 8,14,15 <==

Answer 2

we have

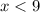`x<9` ------> inequality A

The solution of the inequality A is the interval--------> (-∞,9)

All real numbers less than
`9`

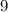
`x\geq14` -----> inequality B

The solution of the inequality B is the interval--------> [14,∞)

All real numbers greater than or equal to
`14`

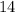
The solution Inequality A or Inequality B is equal to

Solution A+Solution B

(-∞,9)U[14,∞)

The solution of the compound system of inequalities must satisfy inequality A or inequality B

we're going to verify every case

case A)
`\$8`

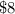
Substitute the value of x in the inequality A and in the inequality B to verify

Verify inequality A

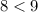`8<9` -------> is true

Therefore

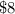`\$8` is a possible value for x

You don't need to check for inequality B

case B)
`\$9`

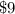
Substitute the value of x in the inequality A and in the inequality B to verify

Verify inequality A

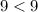`9<9` -------> is not true

Verify inequality B

`9\geq14` ------> is not true

Therefore

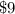`\$9` is not a possible value for x

case C)
`\$11`

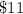
Substitute the value of x in the inequality A and in the inequality B to verify

Verify inequality A

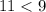`11<9` -------> is not true

Verify inequality B

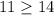`11\geq14` ------> is not true

Therefore

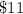`\$11` is not a possible value for x

case D)
`\$13`

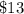
Substitute the value of x in the inequality A and in the inequality B to verify

Verify inequality A

`13<9` -------> is not true

Verify inequality B

`13\geq14` ------> is not true

Therefore

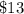`\$13` is not a possible value for x

case E)
`\$14`

Substitute the value of x in the inequality A and in the inequality B to verify

Verify inequality A

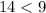`14<9` -------> is not true

Verify inequality B

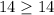`14\geq14` ------> is true

Therefore

`\$14` is a possible value for x

case F)
`\$15`

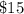
Substitute the value of x in the inequality A and in the inequality B to verify

Verify inequality A

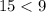`15<9` -------> is not true

Verify inequality B

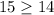`15\geq14` ------> is true

Therefore

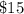`\$15` is a possible value for x

therefore

the answer is

`\$8`

`\$14`

`\$15`