Question

Garden canes have lengths that are normally distributed with mean 208.5cm and standard deviation 2.5cm. What is the probability of the length of a randomly selected cane being between 205cm and 210cm? Correct to 3 decimal places.

Answer 1

Given:

a.) Garden canes have lengths that are normally distributed with a mean of 208.5 cm.

b.) Standard deviation of 2.5 cm.

c.) Probability of the length of a randomly selected cane being between 205cm and 210cm.

Step 1: Determine the z-score of two measures (205 cm and 210 cm).

`z\text{ score of 205 = }\frac{x\text{ - }\mu}{\sigma}\text{ = }\frac{205\text{ - 208.5}}{2.5}\text{ = }(-3.5)/(2.5)\text{ = -1.4}`
`z\text{ score of 210 = }(x-\mu)/(\sigma)\text{ = }(210-208.5)/(2.5)\text{ = }(1.5)/(2.5)\text{ = 0.6}`

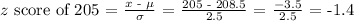
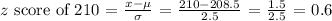
Step 2: Let's determine the equivalent probability of each computed z score.

For 205 cm:

`\text{ Probability of -1.4 z score = 0.0808}`

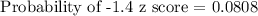
For 210 cm:

`\text{ Probability of 0.6 z score = }0.7257`

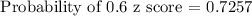
Step 3: Subtract the two probabilities.

`\text{ 0.7257 - 0.0808 = 0.6449 }\approx\text{ 0.645 x 100 = 64.50\%}`

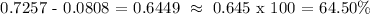
Therefore, the probability of the length of a randomly selected cane being between 205cm and 210cm is around 64.50% or 0.645

Below are the table applied to determine the respective probabilities on a given z score: