We have the compound inequality in one variable: 4x - 4 < 12 and 3x+ 5 < 8.
We can solve them individually and then and see which are the limits for x.
We start with 4x - 4 < 12:

Then, we continue with 3x + 5 < 8:
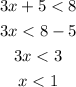
If we combine the two inequalities, we can see that there is no minimum limit for x, but we have two upper limits for x: x < 4 and x < 1.
The last includes the former, as all values that satisfy x < 1 also satisfy x < 4.
Then, the solution interval for this inequality is x < 1.
Answer: x < 1