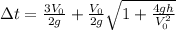Question

A player holds two baseballs a height (h) above the ground. He throws one vertically upward at speed (vo) and the other one vertically downward at the same speed. Determine the speed of each ball when it strikes the ground and the difference between their times of flight.

Answer 1

Final speeds of both baseballs will be the same when they hit the ground, calculated by the kinematic formula, and the difference in time of flight is twice the time it takes for the upward-thrown ball to reach its highest point and start falling.

When a player throws one baseball vertically upward at speed (vo) and another vertically downward at the same speed, the formula to calculate the final velocity (v) at the point of impact, ignoring air resistance, is given by v = √(v₀^2 + 2gh), where g is the acceleration due to gravity (9.81 m/s²) and h is the height from which the balls were thrown.

The ball thrown downwards will have an initial speed of v₀ downwards; therefore its final speed will be v = v₀ + √(2gh).

The ball thrown upwards will reach a velocity of zero before changing direction and falling back down, thus its final speed will converge on the same value as a ball thrown downwards (ignoring air resistance and the initial upward speed).

The difference in time of flight is due to the time it takes for the upward thrown ball to stop and start falling, which is t = v₀/g.

So, the upward thrown ball will take an additional 2t (up and down) time to hit the ground compared to the downward thrown ball.

Utilizing the kinematic equations for projectile motion can aid in solving for these values.

Answer 2

Assume that air resistance may be ignored.
All measurements are positive upward.
g = acceleration due to gravity.

Case A; The ball is thrown vertically upward.
The time, t₁, to reach maximum height is one half of the time of flight.
Because the vertical velocity is zero at maximum height,
V₀ - gt₁ = 0
t₁ = V₀/g.
The time of flight is
t = 2t₁ = (2V₀)/g. (1)
Let v = the vertical velocity with which the ball strikes the ground. Then
v² = V₀² + 2(-g)(-h)
v = √(V₀² + 2gh) (2)

Case B: The ball is thrown vertically downward.
The time of flight, t, is given by
-h = -V₀t + (-g)t²
gt² + V₀t - h = 0
t = 1/(2g)[-V₀ +/- √(V₀² + 4gh)]
Reject negative time

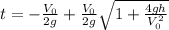
`t=- (V_(0))/(2g) + (V_(0))/(2g) \sqrt{1+ (4gh)/(V_(0)^(2))` (3)

Let v= the speed with which the ball strikes the ground.
-v = -V₀ - gt
v = V₀ + gt

`v = V_(0)- (V_(0))/(2) + (V_(0))/(2)\sqrt{1+ (4gh)/(V_(0)^(2))} \\ v = (V_(0))/(2) (1+\sqrt{1+ (4gh)/(V_(0)^(2)) })`

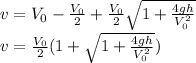
Answer:
The speed with which the ball strikes the ground is
v = V₀√[1 + (2gh)/V₀²], when the ball is thrown upward

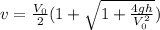
`v = (V_(0))/(2) (1+\sqrt{1+ (4gh)/(V_(0)^(2))})` when the ball is thrown downward.

The difference in time of flight is

`\Delta t = (3V_(0))/(2g) + (V_(0))/(2g) \sqrt{1 + (4gh)/(V_(0)^(2)) }`