Question

My question is:A bacteria culture grows from 10 bacteria at 1.5% per minute starting at 7:00 am. Find the bacteria count after 12 hours if continuous growth is assumed. (Remember to round down to the nearest whole bacterium)

Answer 1

Exponential Continuous Growth

The exponential is commonly used to model natural processes of growth.

The formula of the exponential continuous growth is:

`P=P_o\cdot e^(kt)`

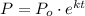
Where:

Po = the initial population of the bacteria culture

k = a fixed constant

t = time

P = the population of the bacteria culture at any time t

The initial population of bacteria is given as Po=10

We are given the growth rate at 1.5% per minute.

The process starts at 7:00 am. At 7:01 am there will be 1.5% more bacteria than the previous minute, that is P=1.015*10=10.15 for t=1, thus:

`10.15=10\cdot e^(k(1))=10\cdot e^k`

Solving for k:

`\begin{gathered} 10\cdot e^k=10.15 \\ e^k=1.015 \\ k=\ln \text{ 1.015} \\ k=0.01489 \end{gathered}`

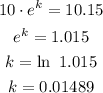
Now we have the value of k, the function is:

`P(t)=10\cdot e^(0.01489t)`

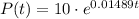
We are required to find the bacteria count after 12 hours. Since the time must be expressed in minutes, t=12 hours = 12*60 = 720 minutes

`P=10\cdot e^(0.01489\cdot720)=10\cdot45,242.9=452,429`

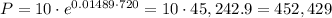
The bacteria count will be 452,429 after 12 hours